作者：时光
审核：东达

相信很多朋友们第一次接触“程序绘画”是在小学时期信息技术课，课本上介绍了一种名叫海龟绘图（Turtle Graphics）的有趣软件。回想一下，我们是怎么让小海龟运动起来的？答案是：利用代码。1996年，Seymour Papert和Wally Feurzig发明了一种专门给儿童学习编程的语言——Logo语言，我们正是利用这种语言指挥海龟在屏幕上绘图的。然而随着时代的发展，Logo已经渐渐淡出人们的视线，主流的绘图方式也发生了改变。

本文介绍的是如何利用着色器（下文写作Shader）语言达成绘制3*3棋盘格效果，笔者在这里借助了UE4进行演示。如果感兴趣的话可以在Unity或者其他在线渲染网站（例如ShaderToy）中利用本文例举的算法进行尝试。

为什么程序绘画的第一篇文章讲的是棋盘呢？因为棋盘格子的绘制是程序绘画中较为基础的部分，原因是实现这个效果的算法比较简单，可以通过演算轻松的得到结果，对感兴趣但又不是很了解Shader的同学比较友好。不过由于涉及到一些术语，这篇文章推荐有一定计算机图形学基础的同学阅读。那么话不多说，我们正式开始吧！

开始绘制

打开我们强大的UE4的Shader Graph，我们正式准备开始绘图。首先我们要做的事情是将texcoord（一组纹理坐标）节点连接到输出根节点的base color上，会得到以下效果：

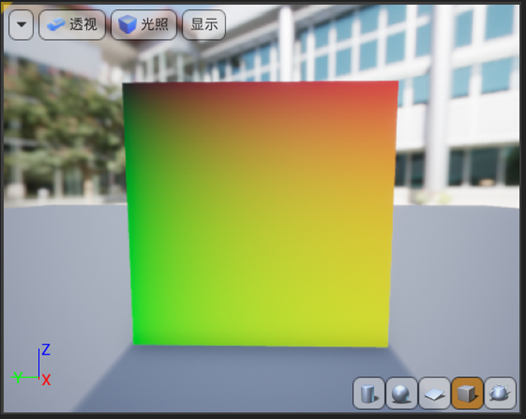
这是个什么东西，它是怎么得到的？（怎么说呢，它看起来真的很像某种水果。）首先我们要明确的是：texcoord节点储存了一组纹理坐标，它的范围从0 ~ 1。如果我们以图1中的矩形的左上角为原点建系，并且让y轴指向下方，那么texcoord对应的(0, 0)坐标就指的是左上角，(1, 1)指的就是右下角。同时，我们将texcoord节点连接到了base color上，后者需要一个Vector3类型的变量（分别指代颜色的RGB）作为输出，而texcoord的纹理坐标是一个Vector2类型，差了一个分量。幸运的是引擎很聪明地自动帮我们加上了0作为第三个分量，所以实际上左上角对应的颜色是(0, 0, 0)，即黑色；右下角对应的颜色是(1, 1, 0)，即黄色。

为了进一步验证我们的想法是否正确，可以手动把 “1” 作为第三个分量，当输入进base color后，我们会得到下图所示的结果。在下图的情况下，左上角的输出是(0, 0, 1)，右下角的输出是(1, 1, 1)，符合预期结果。

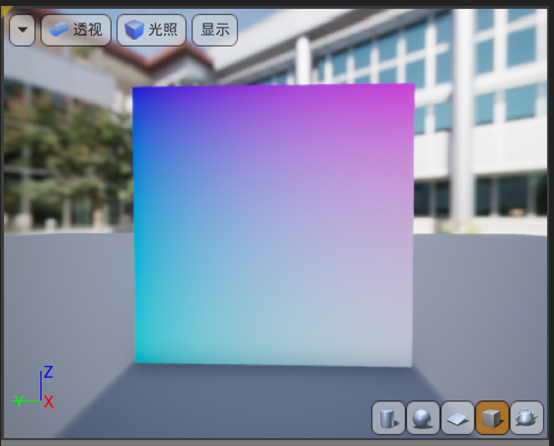
数学处理

现在我们的数据呈现完美的连续状态。如果我们想要得到分明的棋盘格子的话，这意味着我们需要把连续的数据转变成“平台”。在这里，我们可以通过引入Floor函数对坐标进行取整来实现。Floor函数可以把小数向下取整，得到一段数据。但是我们需要三行三列格子，怎么办呢？我们可以通过乘以3得到3段数据，如下所示：

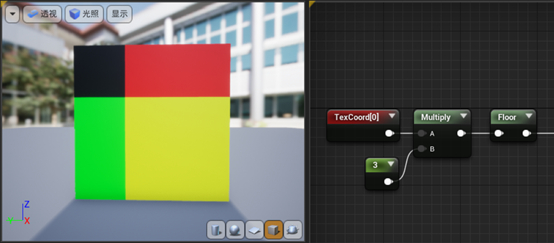
看上去效果不太对？原因是颜色分量超出1的部分被按照1来计算了，所以出现了区域颜色一致的情况。实际上右下角的格子的数据是(2, 2, 0)，但输出的效果却是(1, 1, 0)，便得到了黄色。如果我们对这些数据除以2，就可以让九宫格的颜色区分开来，如下所示：

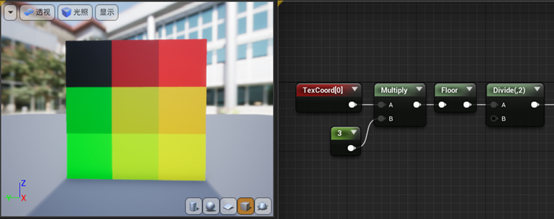
我们离最终的效果已经很接近了。观察一下现在的棋盘，每个格子的数据分别是：

1
2
3

(0, 0, 0)      (0.5. 0, 0)      (1, 0, 0)
(0, 0.5, 0)    (0.5. 0.5, 0)    (1, 0.5, 0)
(0, 1, 0)      (0.5. 1, 0)      (1, 1, 0)

相信你一定已经发现其中有趣的规律了。如果我们针对每个格子单独输出其R通道的值，就会得到黑灰白三色的竖条（如下图所示）；如果我们针对每个格子单独输出其G通道的值，就会得到黑灰白三色的横条：

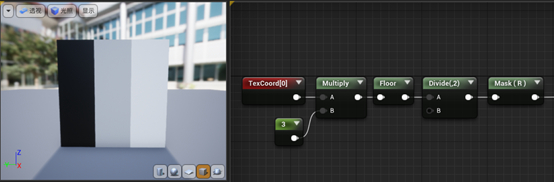
如果我们把R通道和G通道相加是不是就可以得到棋盘格子了呢？不，我们会得到下图所示的结果：

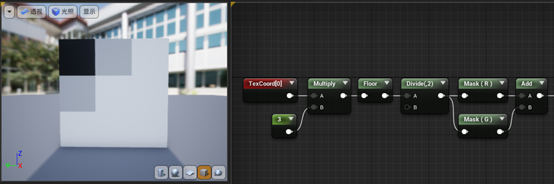
结果很不尽人意，这是因为超出的部分都被自动变成了1。同时棋盘雏形上还有灰色的块，而我们想得到的是一个黑白的棋盘，也就是说最终输出的颜色只能有(0, 0, 0)和(1, 1, 1)。怎么实现黑白的效果呢？其实现在九宫格的数学结果是这样的：

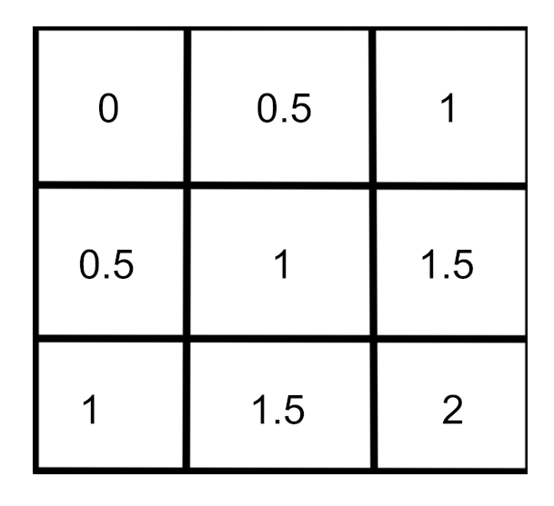
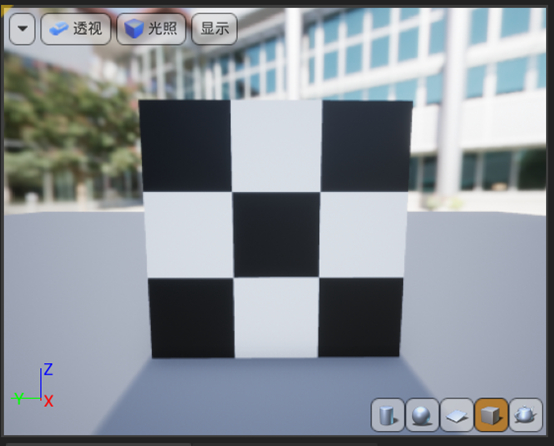
这时候我们只要取小数就能得到相对理想的“灰白棋盘效果”了。想要得到“黑白棋盘效果”，我们只需要对(0.5, 0.5, 0.5)的灰色乘上2即可。最终得到的效果如图所示。如果我们希望增加棋盘的行列数，可以在前面进行floor操作时给texcoord乘上更大的值。