作者:我本张逸仙
作者知乎主页链接:Thinker
变分推断
基本思路就是:在概率模型中,经常需要近似难以计算的概率分布。对于所有未知量的推断都可以看作是后验概率的推断(因为贝叶斯公式可以构造):
p(x)=∑p(x∣z)p(z)
对于大量数据而言,马尔可夫蒙特卡洛方法就太慢了,因此就需要用到变分推断法。
这里经常遇到的是两种变量,一个是real data:x,还有一个是latent data: z。
那么构造的推断问题就是:输入数据的后验条件概率分布p(z∣x)的得知。通过ELBO的方法,希望找出一个真实的分布q(z),用这个真实的分布来近似代替真实的后验分布p(z∣x)。
因此需要优化的是它们的KL散度:
q∗(z)=argminq(z)∈QKL(q(z)∣∣p(z∣x))
而KL散度值也可以进一步改写:(下面的期望均是对q(z)的期望)
KL(q(z)∣∣p(z∣x))=E(logq(z))−E(logp(z∣x))=E(logq(z))−E(logp(x,z))+logp(x)
因此,定义evidence lower bound(简称ELBO):
ELBO(q)=E(logp(z,x))−E(logq(z))
当然了,上面的q(z)可以换q(z∣x),那么等式只需要稍加修正一下即可:
不论是在VAE,GAN还是在NF里面,总有一个不等式特别重要:
- 让pθ(z∣x)与qϕ(z∣x)尽可能近似
DKL(qϕ(z∣x)∣∣pθ(z∣x))=log(pθ(x))−z∑qϕ(z∣x)log(qϕ(z∣x)pθ(x,z))=log(pθ(x))−L(θ,ϕ;x)
该方程想要DKL尽可能接近于0,就是让他们俩个尽可能地接近,因此,继续做转换得到:L(θ,ϕ;x)=Eqϕ(z∣x)[log(pθ(x∣z))]−DKL(qϕ(z∣x)∣∣pθ(z))
所以,把两个等式联立,就可得到:log(pθ(x))−DKL(qϕ(z∣x)∣∣pθ(z∣x))=Eqϕ(z∣x)[log(pθ(x∣z))]−DKL(qϕ(z∣x)∣∣pθ(z))
而目标是要让DKL(qϕ(z∣x)∣∣pθ(z∣x))尽可能接近于0,因此可以得到论文中的等式:log(pθ(x))≥Eqϕ(z∣x)[log(pθ(x∣z))]−DKL(qϕ(z∣x)∣∣pθ(z))=−F(x)
上面的公式便是变分推理的重要的地方。这里的F被称为ELBO界
VAE (变分自编码器)
VAE是想要上面求解的ELBO尽可能地大,它提出了SGVB和重参数方法。
VAE的网络架构图如下所示:

简单来说,它是输入real data x,通过一个生成网络h,g生成想要得到的μx,σx:
μx=g(x)σx=h(x)
再引入一个高斯噪声N(0,1),两者相构造latent变量z(重参数技巧,这样可以反向传播了)
z=σxζ+μx
然后z再通过decoder解码成x^:
x^=f(z)
注意:VAE在做的时候,要保证z是一个正态分布,因为这是它和AE一个很大的不同点,它能保证潜在空间是有一定的规律性–>连续性、完整性。
VAE的损失函数是:
L(θ,ϕ;x)=ELBO=Eqϕ(z∣x)[log(pθ(x∣z))]−DKL(qϕ(z∣x)∣∣pθ(z))
这里的第一项可以理解为重构的损失,第二项可以理解为regularization loss
用极大似然法去处理第一项,得到的答案就是:
(f∗,g∗,h∗)=argmax(f,g,h)∈F×G×H(Ez qx(−2c∣∣x−f(z)∣∣2)−KL(qx(z)∣∣p(z)))
第二项怎么处理呢?直接积分求解即可:
−DKL(qϕ(z∣x)∣∣pθ(z))=∫qθ(z)(logpθ(z)−logqθ(z))dz=21j=1∑J(1+log((σj)2)−μj2−σj2)
(注意,因为是要尽可能使得z的分布接近于N(0,1),因此z分布的均值是0,方差是1;而对于qϕ(z∣x)而言,它是N(μ,σ)分布的)。
第二项的意思就是尽可能地让qϕ(z∣x)往N(0,1)上靠,第一项的意思就是生成的x^和x的MSE,第一项其实就是AE有的项;第二项就相当于一个正则化项。
如果你想要生成一个全新的图片的话,直接对z进行sampling,然后代入decoder网络,就可以得到一个全新的图片了。
GAN (对抗学习)
GAN是一个生成器G–generator网络和一个判别器D-discriminator网络构成的:

GAN可以认为是使用的是交叉熵的公式来判别分布的相似的:
H(p,q)=−i∑pilogqi
这其实就像是一个二分类问题,数据要么从real data中得到,要么直接随机生成一个noise然后通过generator得到。那么discriminator就需要判断它到底是real还是fake的:
discriminator就只说:对,错。就是一个二分类网络。
假定 ![[公式]](https://www.zhihu.com/equation?tex=y_1) 为正确样本分布,那么对应的(
为正确样本分布,那么对应的( ![[公式]](https://www.zhihu.com/equation?tex=1+-+y_1) )就是生成样本的分布。
)就是生成样本的分布。 ![[公式]](https://www.zhihu.com/equation?tex=D) 表示判别器,则
表示判别器,则 ![[公式]](https://www.zhihu.com/equation?tex=D%28x_1%29) 表示判别样本为正确的概率,
表示判别样本为正确的概率, ![[公式]](https://www.zhihu.com/equation?tex=%EF%BC%881+-+D%28x_1%29%29) 则对应着判别为错误样本的概率。
则对应着判别为错误样本的概率。
因此用交叉熵来实现它就是:
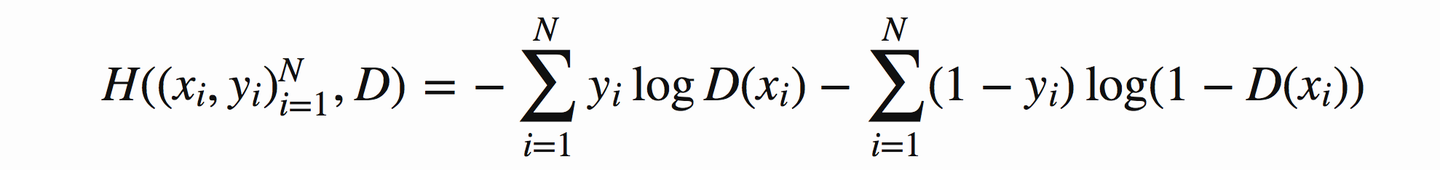
这里设生成器生成的样本x^~G(z),z是服从于投入生成器中的噪声的分布。x是真实的样本点。
推广到无穷大,改写为积分形式。
下面是正式的流程:
我们首先固定G(就是给一个任意的G),然后要得到的就是V(G,D)
V(G,D)=∫∞pdata(x)logD(x)dx+∫∞pz(z)log(1−D(g(z)))dz=∫∞(pdata(x)log(D(x))+pg(x)log(1−D(x)))dx
然后对积分式里面的求导,就可以得到最大的V(G,D),也就是此时D最牛逼了:
此时:
D∗(x)=pdata(x)+pg(x)pdata(x)
即:
V(G,D)=Ex−>pdata[pdata(x)+pg(x)pdata(x)]+Ex−>pg[pdata(x)+pg(x)pdata(x)]
然后此时又要不断的训练生成网络generator,让maxDV(G,D)=V(G,D∗)最小:C(G)=minGV(G,D∗)
因此:当pg=pdata=1/2(纳什均衡,此时你可以认为它已经分不清楚谁是谁了)的时候,就得到了最小值了:
GminDmaxV(G,D)=GminV(G,D∗)=−log4
此时,代入他们的最小值,改写:
C(G)=−log(4)+KL(pdata∣∣2pdata+pg)+KL(pg∣∣2pdata+pg)=−log(4)+2JSD(pdata∣∣pg)
当JSD为0的时候,就认为pdata和pg相等了,就分不出彼此来了。此时C* = -log4
NF (流模型)
标准化流是另外一种生成网络,它基于一个空间变化的定理。
我们假设生成网络还是G,z是一个标准的正态分布–latent变量,而x是real data。
Z−>Generator...−>x
因此希望生成的x的分布与x的初始分布越接近越好
假设{x1,x2,...,xm}是来自pdata(x)的一个sampling
希望pG(x)与pdata(x)越接近越好,也就是有一个target:
G∗=argmaxGi=1∑mlogPG(xi)≈argminGKL(pdata(x)∣∣pG(x))
这里有几个数学公式:线性变换之后的体积等于转换矩阵的行列式
![[公式]](https://www.zhihu.com/equation?tex=y%3Df%28x%29%5C%5C+p%28y%29%3Dp%28f%5E%7B-1%7D%28y%29%29+%5Ccdot+%5Cleft%7C+%5Cdet%28J+%28f%5E%7B-1%7D%28x%29%29%29+%5Cright%7C+%5C%5C+%5Clog+p%28y%29%3D%5Clog+p%28f%5E%7B-1%7D%28y%29%29+%2B+%5Clog+%5Cleft%7C+%5Cdet%28J+%28f%5E%7B-1%7D%28x%29%29%29+%5Cright%7C+)
也就是说,行列式可以被认为是变换 ![[公式]](https://www.zhihu.com/equation?tex=y%3Df%28x%29) 的局部线性体积变化率
的局部线性体积变化率
NF的输入与输出的size必须相同,这是与其他俩个不一样的,因为其他几个都是可以随意输入的。
然后假设它是一系列的Flow网络组成

因此对原网络进行修改:
logpK(xi)=logπ(zi)+h=1∑Klog∣det(JGK−1)∣
要求左边等式的最大值–>log likelihood最大
那么要想求的话,可以反过来去考虑,通过x进入G−1网络生成z。
由于上面那个式子的计算量太复杂了,因此需要做下面的处理:
1. Coupling Layer: – > 用在NICE 和 Real NVP里面的

它让前1:d的直接从z->x,而后边的d+1:D的就要通过前边的数据经过F和H网络求解βd+1:D和γd+1:D,经过线性叠加:
xd+1:D=βd+1:D×zd+1:D+γd+1:D
而经过coupling layer后的贾克比矩阵就称为了一个三角矩阵:
`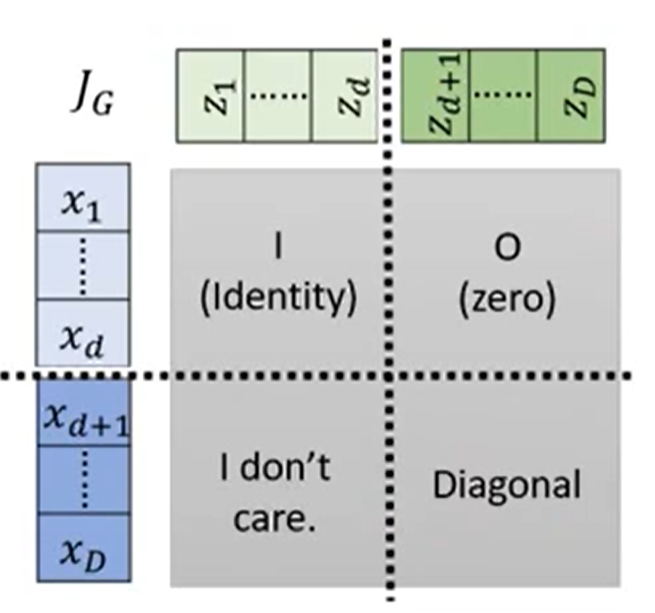
因为上面的是直接copy过去的,就是1:1;而右下角的对角线上的值(D>i>d+1)就是βi值
因此,贾克比矩阵的行列式即可写出:
det(JG)=1×1×...×1×βd+1×...×βD
但是如果每一个网络都按照这样子去处理,那么是不是前d项都不会发生变化?
因此必须要交错的去处理它,每一个网络随机选取d项,且d的大小也需要不一样,这样stacking起来后才会有效果。

- 1x1 Convolution
除了耦合层以外,还可以使用一维卷积,这个是GLOW提出来的,效果特别好。
假设是在处理图像,因此是有3个channels的,RGB三个通道嘛。用到的一维卷积就是一个3x3的矩阵W:
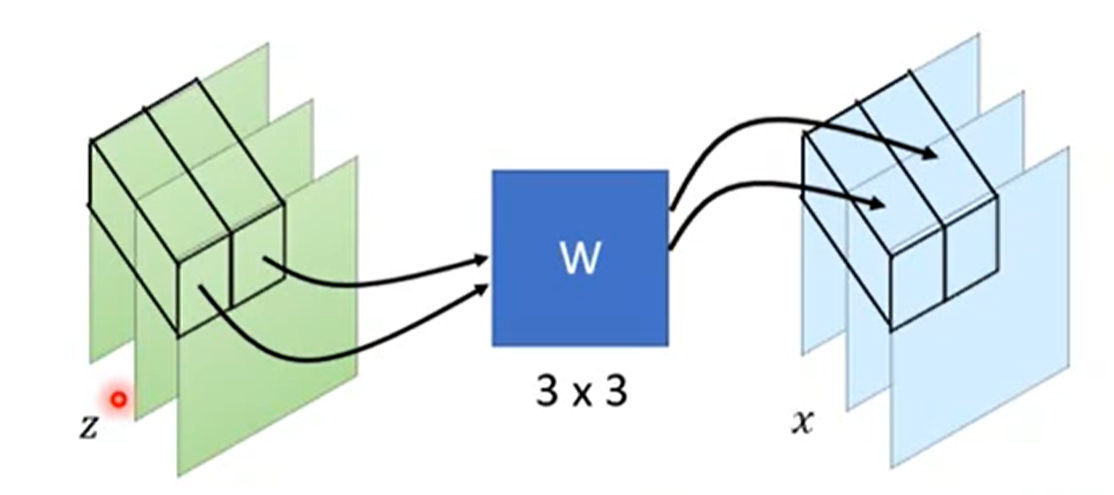
通过一维卷积后,size是不会发生变化的,而这个W矩阵其实就是det(JG):
x=f(z)=W×z
\begin{equation} %开始数学环境
J_f = \left( %左括号
\begin{array}{ccc} %该矩阵一共3列,每一列都居中放置
w_{11} & w_{12} & w_{13}\\ %第一行元素
w_{21} & w_{22} & w_{23}\\ %第二行元素
w_{31} & w_{32} & w_{33}\\
\end{array}
\right) = W %右括号
\end{equation}
只要W是好求解的,那么结果也就很好求解:

因此结果就是,对角线上的W矩阵相乘:
(det(W))d×d
替换公式:
logpK(xi)=logπ(zi)+h=1∑Klog∣(det(W))d×d∣
这样就将复杂运算简单化了
参考:
[1] 李宏毅机器学习
[2] 苏剑林


为正确样本分布,那么对应的(
)就是生成样本的分布。
表示判别器,则
表示判别样本为正确的概率,
则对应着判别为错误样本的概率。
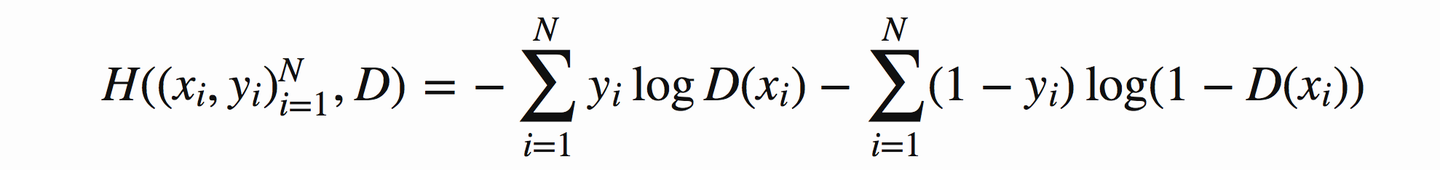
的局部线性体积变化率











